Blog 07-20-25: Inverse Matricies

Currently Listening to:

Blog Post 07-20-25: Inverse Matrices

I've been thinking alot about Inverse Matricies lately. Not by choice really. I feel like I just don't get it so it haunts me. Like a spectre. A spectre that haunts europe only I'm europe and the spectre haunts me as I've explained before.

This is because I was working on that LU Decomposition calculator earlier this week. I got it out of a textbook. It reccomended I use Crout's method for LU Decomposition, with partial pivoting. With partial pivoting? I'm going to be honest I struggled with partial pivoting in school. I remember there was only like 3 youtube videos about it. And that was for Gauss-Jordan Elimination with partial pivoting. I still don't fully understand it. But in the book I noticed it said:

Incidentally, if you ever have the need to compute $\textbf{A}^{-1} \cdot \textbf{B}$ from matrices $\textbf{A}$ and $\textbf{B}$, you should LU decompose $\textbf{A}$ and then backsubstitute with the columns of $\textbf{B}$ instead of the unit vectors that would give $\textbf{A}$'s inverse. This saves a whole matrix multiplication, and is also more accurate.

- Numerical Recipes in C, Second Edition

This was strange to me, since the code I had used to calculate the LU decomposition didn't use backsubstitution. But then again, I did not use their algorithm, since they relied on strange libraries. I instead just read what they had done mathematically.

I have the second edition, so I got a similar book, Numerical Recipes: the Art of Scientific Computing, from [REDACTED], and here they actually explain the Gauss-Jordan routine has the same as this idea.

Alternatively, there is nothing wrong with using a Gauss-Jordan routine [...] to invert a matrix in place, destroying the original. Both methods have practically the same operations count.

- Numerical Recipes: The Art of Scientific Computing

I am not sure what to think of this. So I will try it out myself.

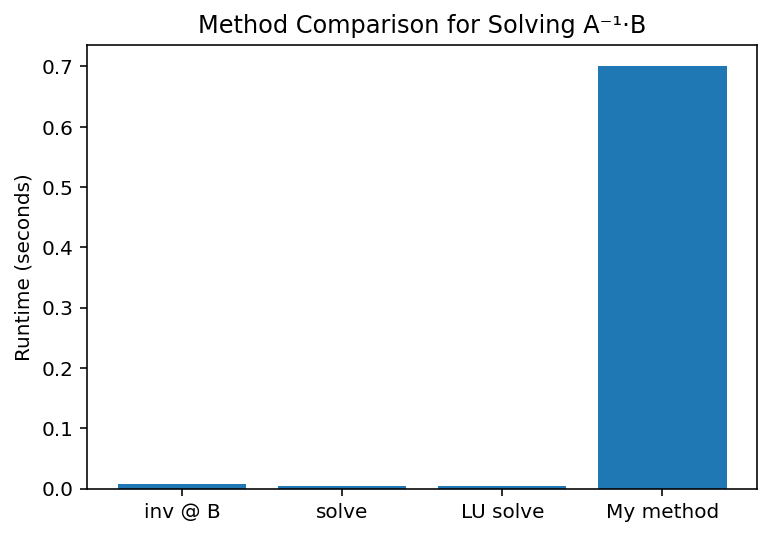
4 methods for solving inv(A) dot B. My method is significantly higher than accepted methods.

shut up.

Needless to say, I don't think I did the method correctly, despite my best efforts. But to be fair the other methods were from built in modules who've had hundreds or thousands of CS-major eyes on them and mine I made trying my best to convert C to Python.

I could always just give up and use Gauss-Jordan, but I really do want to know what I did wrong. I decided to check the code for scipy's LU solve. The code I did for that was just:

Python

from scipy.linalg import lu_factor, lu_solve
lu_solve(lu_factor(A), B)

After investigating the code for scipy's LU solve, I found that these use lower level libraries, with scipy using LAPACK. This gives me a good idea that I don't want to do now but in the future. With me I found several GPUs in the trash over at my old school. I think I can gerrymander these together and use OpenACC to run some code in C.

I tried running my code in PyPy and the perfomance time doubled. I don't know how. Do not ask me. I tried it again with pypy3 and that still did not work. In conclusion, the fastest way I have currently to find the inverse and multiple of 2 matricies is scipy, though I prefer numpy since the times are on average the same, and I understand numpy's C code, none of scipy's fortran. Though I will not give up. When I get my hands on some PCIe cables and a power supply, it will work. I will find this result.